Math with Bad Drawings has a post about “word problems” that will sound very familiar to anyone who’s taught introductory physics. As he notes, the problem with “word problems” for math-phobic students is that it requires translating words into symbols, and then using the symbols to select a procedure. It adds a step to what at a lower level is a simple turn-the-crank algorithm: given this set of symbols, do these abstract operations, and write down the answers.
This is a very familiar problem in intro physics, where I regularly have struggling students tell me “I can do the math just fine, I just don’t know how to set up the problems.” And, you know, that’s true, because the math is far and away the least difficult part of intro physics– it’s all arithmetic and algebra, with a tiny bit of trigonometry sprinkled in. We very occasionally use stuff from calculus, but almost never at a level above the routine algorithms for differentiation and integration.
All of the problems in intro physics are word problems, because that’s where all the action is. The hard part is figuring out how to translate a real-world situation into symbols, and where to make approximations and idealizations to make that process easier. Once you have all the symbols, there are simple heuristics to figure out what procedures to try, but it’s getting the right symbols in the right places that’s a problem.
And there’s always a tension here, when it comes to writing homework and exam questions. On the one hand, we want to be testing students’ understanding of the concepts and procedures of intro physics, which argues for very abstract, very plainly stated problems– blocks sliding on inclined planes, uniformly charged spherical shells, etc. But on the other hand, I think probably the most important thing physics has to offer is the idea that sometimes the spherical cow is good enough, that very translation and abstraction process that you find in “word problems.” Which argues for much more rich-context stuff.
And, in the end, the only way to get that process down is to do it– to work a whole bunch of different “word problems” until you get comfortable with the idea of translating and abstracting. Because sooner or later, students who go on in physics will need that. The alternative is to give clearly stated problems and explicitly teach the heuristics for making decisions, but that just kicks the can down the road to the next class.
One way to ease this, though, is to move some of that translation and abstraction process up a bit, to earlier ages. which is where this pivots to become another Thanks, Common Core post, based on a conversation I had last night with SteelyKid, after sparring class at taekwondo. We were at Panera, and I asked her a math question (as one does with one’s first-grader…): “What’s 27 minus 19?”
“Ummm… Can you write that down?” she asked. So I wrote the top lines in this picture:

(OK, technically, this is my re-creation of what we drew on the back of a Panera receipt last night, but roll with it…)
“OK, I’m going to re-write that as a number sentence,” she said, and produced the second line. “27 take away 19 equals what?”
Then she went on to the third line, saying “So, what I do is, I break the 27 up, so it’s a 2 and a 7, which means 20 and 7…” and though she stumbled for a second at this point, she quickly got that 20 minus 19 leaves 1, which you combine with the 7 to make 8, the correct answer.
That’s not by any means the traditional algorithm I learned (which would start from the top-line format), but it works, and she was very pleased with herself. What I like about it, though, is that this is already getting across the idea of translating between representations. These are all the same problem, stated in words and translated into symbols, but she recognizes that you can write the same problem in different ways, and that that’s a useful thing to do. It’s turning a numbers-and-symbols problem into a “word problem” and back again, and I think that’s great.
That doesn’t mean this will automatically translate to being able to turn rich-context physics problems about real bodies in motion into abstract collections of point masses connected by massless springs, but this kind of thing is a good start. Carry it on up through the curriculum, and teaching intro physics to incoming college students who learned math this way could get a lot more pleasant.
So, as with last week’s post: Thanks, Common Core. More like this, please.
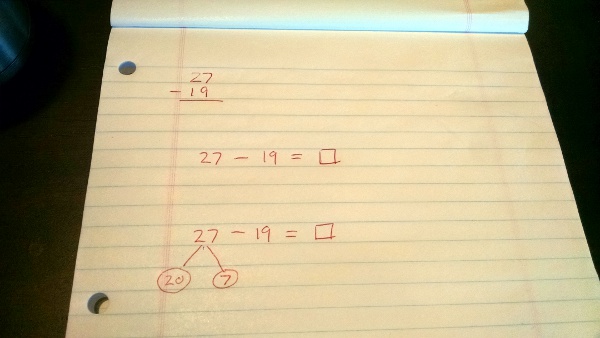
“Sometimes the spherical cow is good enough.”
Great quote!
The fact that SteelyKid can already turn a number sentence into a word sentence and back again (at least as you report it) puts her a step ahead of my former high school physics students. (I’m pretty sure I’ve commented about this before, my apologies for repetition.) They complained that they weren’t good at “word problems” when I wrote “What force is needed to accelerate a 5kg mass at 3 m/s/s?” They also got really tired of me saying “Life is a word problem.” Most of that class did fine in the math class across the hall and most of the parent’s loved our math teacher because she was so good. She was for values of good that equal taking a D math student and making them a B math student (and not because she went easy on them). But as far as I could tell she did not teach the kids to apply the math, to anything.
There definitely seems to be an “industry” of curricula and teaching materials aimed at supporting the Common Core standards.
My daughter (also in first grade) has been learning both math and reading in ways quite different than I remember, but quite similar to what you’ve described with SteelyKid.
One very nice tool is the “part-part-whole” box. It consists of a square divided into three boxes: two smaller ones at the top and a larger one below. The bottom box is always the sum of the upper two, but the teacher (or the worksheet) can have _any_ two out of three boxes filled in. The students both have the immediate goal of “filling in the blank”, but also are asked to rewrite the problem as an equation.
So the students are learning from the very start about the relationship between addition and subtraction: 3+5 = 8, 5+3 = 8, 8-3 = 5, 8-5 = 3, are all identical statements about a numerical relationship. You can go from “What is eight minus three?” to “Three plus what makes eight?” and they mean the same thing.
I definitely think this kind of toolkit is going to serve this cohort well in the future. It takes the very concrete number problems (which are critical for learning) and layers them on a very general, abstract concept about numeracy. That layering and abstraction is exactly what is needed to solve “word problems,” just as you say.