Yes Virginia, There Are Quantum Jumps

In a weird coincidence, shortly after I wrote a post about “quantum leap” as a metaphor, I was looking up some stuff about John Bell and ran into mentions of a paper he wrote called “Are There Quantum Jumps?” Bell is borrowing a title from Schrödinger, who wrote a pair of articles (really, one article in two pieces) for the British Journal for the Philosophy of Science in 1952 expressing his discontent with the entire idea of “quantum jumps” between states. Bell even opens his paper with a quote from Schrödinger: “If we have to go on with these damned quantum jumps, then I’m sorry that I ever got involved.”

This jogged a memory from my long-ago atomic physics class with Bill Phillips, where he specifically talked about the experimental demonstration of quantum jumps. And that, in turn, seemed like a good excuse for another physics post.

Whoa. Two in one week? I know, it’s shocking. I’m sort of between other projects, though, so can devote a little time to science-y blogging, as opposed to griping about the culture of academia.

Well, whatever the reason, I’ll take it. So, what’s the issue, here? Well, Schrödinger was famously dissatisfied with the Copenhagen interpretation of quantum physics. He was never happy with the theory on a philosophical level, because a lot of it runs counter to classical intuition– the probabilistic nature of the theory and issues of entanglement (both of which are involved in the (in)famous cat problem) put him off the theory entirely.

In the specific case of quantum jumps, he’s complaining about the discontinuities of the theory, namely that you have “stationary state” solutions where an electron orbits happily, and atoms absorb and emit light only in discontinuous jumps between those states. He felt this was a deeply unsatistfying state of affairs, and said so at great length.

But isn’t that, like, the starting point of the quantum theory of atoms? That’s part of the problem Schrödinger had with the whole business– he regarded it as a holdover from the “old quantum theory” period between Bohr’s 1913 introduction of a quantum model of the atom and the late 1920’s when Heisenberg’s matrix mechanics, Schrödinger’s own wave equation, and then the Dirac equation put quantum mechanics on a solid mathematical footing. All the stuff about discontinuous jumps seemed to him like an ad hoc insertion that muddied up the nice picture of those equations, where you have a wavefunction that evolves smoothly in time according to nice equations.

And people were still arguing about this in Bell’s day? Hell, people are still arguing about it today.

In fairness to Bell, his 1987 paper is from a collection in honor of Schrödinger, and he’s mostly just lifting old Erwin’s title and grafting it on to some musing about the Ghirardi, Rimini, and Weber spontaneous-collapse theory (wayyy more detail), which adds some parameters to Schrödinger’s famous equation to get a Copenhagen-ish collapsing wavefunction in a more natural way. But yes, people were arguing about this exact issue for a long, long time.

And this is why it came up in your class? Right. Bill’s class was an introduction to the main issues of modern atomic physics/ quantum optics (there’s a semantic debate there that I could go on way too long about), and we spent a lot of time on the density matrix formulation. Which provides a nicer way to deal with dissipation through things like photon emission than the Schrödinger equation with some discontinuous jumps grafted on.

But then, isn’t the problem solved? Not really, because the density matrix approach, while it has a lot of nice features, is still fundamentally a continuously evolving system. And, at least in Bill’s telling, this continued to pose a problem regarding the existence of quantum jumps– if the density matrix for the system evolves smoothly and continuously, some people argued that there must not be real, discontinuous jumps.

Bill, being an experimentalist by training an inclination, came down decisively in favor of quantum jumps being real, and regarded the question as settled thanks to a couple of experiments in 1986.

So, how do you settle this experimentally? Well, the experimental factor that normally muddies things up is that you’re usually dealing with large numbers of atoms. Which is part of why you use the density matrix in the first place– it is, in some sense, a way of tracking the average behavior of a large ensemble. And if you’re looking at a large ensemble, the emission of a photon or two doesn’t really change the overall energy balance all that much, so you could argue that things are really continuous.

The 1986 papers, one from Dave Wineland’s group at NIST (and check out that high-power author list), the other from Hans Dehmelt’s group, fix this by looking at a single atom at a time, and showing that it undergoes sudden changes of state.

How did they do that? Well, they weren’t dealing with neutral atoms, but ions– mercury in Wineland’s case, and barium in Dehmelt’s– held in an ion trap. These traps are strong enough to confine single articles for extremely long times– days, weeks, months– and since they know exactly where the particle will be, they can focus sensitive detectors on that spot and pick up the light that a single ion emits.

Oh, so they just watched to see that photons only come out one at a time? Well, they did that, but that’s not the proof of discontinuous state changes; that just proves that photons are particles. To demonstrate quantum jumps, they had to turn the photon emission on and off.

OK, what? They used a technique called “quantum shelving,” that relies on the fact that the atoms are not simple two-level systems, but have lots of different energy states. In the mercury case (which I’ll discuss in more detail because that paper is free to read; the idea is the same for the barium experiment), the relevant levels look like this:

There are three sets of levels here: the ground state (bottom of the figure), a “P” state in the upper left, and a “D” state in the upper right.

Why those letters? Oh, God, don’t even go there. Just consider them arbitrary labels and let’s move on.

The important thing here is that the “P” levels interact very strongly with light, and readily absorb photons with a wavelength of about 194 nm. This also means that they readily emit photons, dropping back to the ground state after about two nanoseconds. When they shine in the 194 nm laser, they see lots and lots of photons spraying out, millions of them per second.

The “D” states, on the other hand, don’t interact with the light as strongly. You can move a ground-state ion to the “D” state by getting it to absorb a photon at about 281nm, but it’s much harder to do. And once it’s there, it tends to stay there for a long time, about a tenth of a second, before it emits a 281 nm photon and returns to the ground state.

And this helps you, how? Well, when the ions are in the “D” state, they can’t absorb any of the 194 nm laser light. Which means they stop emitting light until they drop back into the ground state.

And that gives you a way to look for the discontinuous quantum jumps. They trap a single ion, shine in the 194nm laser so it emits a lot of light, and then add some 281nm light as well. Most of the time, the ion just bounces back and forth between the ground and “P” states, spraying 194nm photons all over the place, but every now and then it makes a transition to the “D” state, and stays there for some time. You know this has happened when the 194nm light cuts off, and you know it’s come back when the 194nm light turns back on.

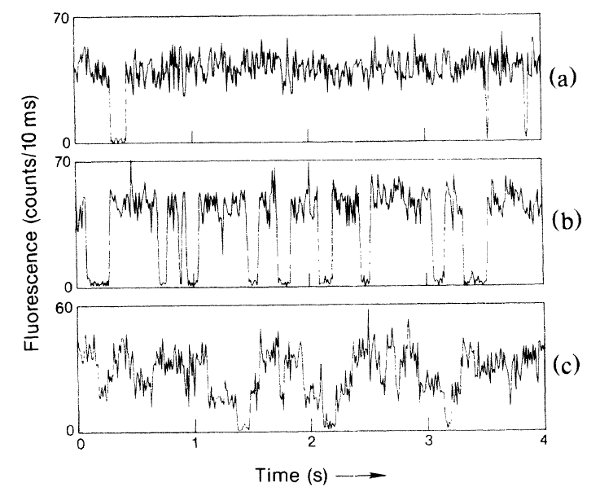
And they saw quantum jumps this way? Yep. The relevant figure looks like this:

The top shows the fluorescence from a single trapped ion over several seconds, to demonstrate that it’s mostly constant (the one period where it shuts off they attribute to a collision with background gas). The middle part of the figure shows a single ion illuminated by both lasers, and you see lots and lots of discontinuous jumps.

So the light cuts off abruptly when the ion moves to the “D” state, and comes back on abruptly when it comes back? Exactly. And the fact that these are abrupt transitions of a single atom shows that this is a discontinuous process– if there were smooth, continuous evolution going on, you would see a smoother transition between things. Instead, you have an “on” level and an “off” level, and nothing in between.

That’s pretty convincing evidence of discontinuous quantum jumps, all right. It certainly looks that way to an experimentally inclined physicist like Bill, or me. There are a few loopholes here– to get a good signal, they need to collect photons for long enough that you could argue that the averaging hides a smoother transition, but they’ve continued to develop these techniques, and you can see the same thing on much faster time scales these days. There really is something very discontinuous that happens when a mercury ion moves from the ground state to the “D” state.

So, end of argument? Not really. You can, for example, find a paper dramatically asserting that there are no discontinuities from 1993, well after the Wineland and Dehmelt experiments. I don’t have a good sense of how this issue has continued to evolve in the foundational theory community.

Presumably, the answer would be “continuously.” Yes, well.

Anyway, this is a clever set of experiments, and the thing that immediately came to mind when I saw the paper title “Are There Quantum Jumps?” pop up in a discussion about Bell. And it’s the reason why my immediate mental answer was “Yes, of course there are.”

And as I said the other day, these jumps are both discontinuous and dramatic– the ion goes to a qualitatively different state, one where it can no longer absorb light that it readily absorbed in the original state. Which is also why I’m perfectly okay with the common metaphorical use of “quantum leap” for a dramatic change.

Well, that’s kind of a lot of work to explain a small semantic point, but it’s pretty cool. Thanks. Happy to be of service.

Bergquist, J., Hulet, R., Itano, W., & Wineland, D. (1986). Observation of Quantum Jumps in a Single Atom Physical Review Letters, 57 (14), 1699-1702 DOI: 10.1103/PhysRevLett.57.1699

Nagourney, W., Sandberg, J., & Dehmelt, H. (1986). Shelved optical electron amplifier: Observation of quantum jumps Physical Review Letters, 56 (26), 2797-2799 DOI: 10.1103/PhysRevLett.56.2797