![]() Two papers with a similar theme crossed my social media feeds in the last couple of days. You might think this is just a weird coincidence, but I’m choosing to take it as a sign to write about them for the blog.
Two papers with a similar theme crossed my social media feeds in the last couple of days. You might think this is just a weird coincidence, but I’m choosing to take it as a sign to write about them for the blog.
So, what are these papers, and what’s the theme? One is the final publication of some results I saw at DAMOP and alluded to back in June, and the other is from this post by Doug Natelson. Both look at the transition from few-body to many-body physics.
And this is interesting, why? I mean, isn’t it obvious that you just add some more bodies? OK, I guess that does need a little more explaining. The papers in question get at one of the fundamental difficulties of dealing with real systems in physics, namely that there are generally only two problems we know how to solve exactly: two particles, and an infinite number of particles.
Ummm… I can see how two particles would be easy, but “an infinite number” sounds impossible, dude. It might seem that way, but one of the great things about calculus is that it provides a lot of powerful mathematical tools for dealing with quantities that might seem to be infinite. If you let the number of particles in a system become infinite, lots of parameters that start out discrete and discontinuous become smooth continuous functions, and you can use calculus to get nice answers in the form of equations you can actually write down and solve.
But you never really have an infinite number of particles, do you? Right, that’s the problem. The game is to assert that you’re in the “thermodynamic limit,” where you have so many particles that it might as well be an infinite number. And for most measurable quantities of stuff, that’s a pretty good approximation– you’re talking about 100,000,000,000,000,000,000 particles on up– and the equations you get by assuming an infinite number work very well.
It’s interesting to ask, though, where that kicks in. That is, how many particles do you need to have before you can start using the infinite-limit answers to describe the properties. This is a hard problem to address, because the really nice mathematical tools don’t work for intermediate numbers, and then you need to do things like simulating huge numbers of particles on a supercomputer to try to figure out the answer.
These papers report a couple of new studies that take on this regime, one experimental and the other theoretical.
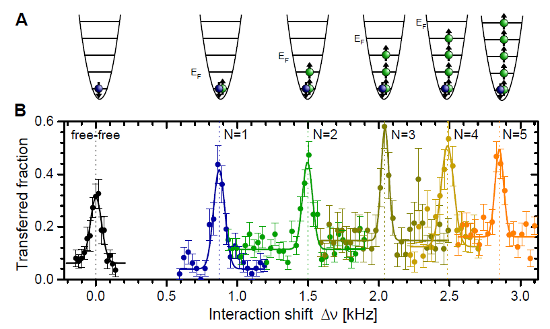
How do you do this experimentally? Isn’t that hard to do? Well, that’s why it’s published in Science (arxiv version). This is a relatively straightforward extension of the paper we talked about back in June, where they showed an ability to prepare a specific number of atoms on demand in a microscopic trap. They use that technique here to prepare samples of zero to five atoms in the same state, and stick in one “impurity” atom in a different internal state.
Why do they do that? Having the “impurity” gives them a single atom they can probe to see the effect of all the others. This is a great system for them to study, because the energy of that one “impurity” atom will depend on its interaction with the others, in a way that’s generally very complicated. They can clearly resolve and measure the shift, though, and see it increasing as they increase the number of atoms, as shown in the “featured image” up top, which I’ll reproduce here:

And how does this show where many-body physics kicks in? Well, there are two cases you can solve exactly: one is the case of a single “majority” atom interacting with the single “impurity” atom, in which case you just have two atoms occasionally knocking into each other, and can solve it exactly. The other case is the limit of an infinite number of “majority” atoms, in which case they provide a continuous background field modifying the energy levels of the impurity.
So, they just measure the shift for different majority numbers and compare to those two limits? Exactly. When they do, they get a graph that looks like this:

This shows the difference between the energy predicted for a single majority atom and the energy measured in the experiment, or predicted by other models. The orange line represents the infinite-number limit, and the green is a supercomputer simulation for the two-majority-atom case.
And the subtle gradations in color of the data points? Match the colors in the first figure, to identify different numbers of majority atoms. Or, if you’re not good at matching colors, you can just count– there are three sets of data points under slightly different conditions, and in each series the points move up and to the left as you increase the number of majority atoms.
So… It looks like they hit the orange line at about four majority atoms? Exactly. The conclusion of this experiment is that, for the purposes of the particular shift they’re measuring, four is effectively the same as an infinite number.
That’s smaller than I would’ve expected. Again, that’s why it’s in Science.
So, what’s the other paper? The other paper, pointed out by Doug, is a theory paper looking at thermodynamic properties of an ideal Bose gas (with a bit more detail in this New Journal of Physics article). What they’re studying isn’t an energy shift, but a phase transition.
Is this one of those cool Star Trek things where you can walk through walls and stuff? Ah, no. That’s comic-book science. This is a phase transition in the sense of moving from gas to liquid or liquid to solid.
That’s not nearly as much fun. No, but it’s real.
In this case, they looked at the behavior of a simulated “box” full of bosons, one of the classic toy models of thermodynamics. They calculated the size of the box for a bunch of different temperatures at a given pressure, using different numbers of particles. Above a particular number, they find that there’s a discontinuity in the volume at a particular temperature.
And this is interesting… why? Well, because that’s what happens when something boils. As you increase the temperature of a liquid, the volume doesn’t change very much until the boiling point, then bam, it shoots way up as the liquid changes to a gas.
When they do their simulation for small numbers of particles, they don’t see that sharp change, just a slow increase up to the “gas” volume. Above a particular number, though, a discontinuity appears, which they interpret as the onset of the collective phase transition.
The number isn’t 4, is it? Um, no. It’s 7616.
That’s kind of random, isn’t it? Well, so is 4, in the grand scheme of things…
Before you ask, though, these aren’t inconsistent results, just different systems. In one case, you’re experimentally looking at a one-dimensional trap of fermions, measuring an energy shift due to collisional interactions between particles, while in the other you’re looking theoretically at a three-dimensional gas of bosons, measuring thermodynamic properties. They’re not really all that similar.
So why are you lumping them together in a single post, then? Well, because they both happened to pass my awareness threshold at the same time, more or less. And also because they’re addressing the same thematic question, namely “At what point can you start thinking about moderate numbers of particles in the same terms you would use for macroscopic samples?”
That has a little bit of a dorm-room stoner sort of sound to it, you know. Yeah, it does, and that’s what’s cool about these. Fifteen years ago, this sort of question would’ve been impossible to discuss outside of physicist bull sessions, tilting toward philosophy, possibly with the aid of mind-altering substances of some sort.
Now, though, thanks to increases in computing power and developments in cold atom technologies, we can start to not only frame these questions in a sensible way, but get actual answers to them. And that’s pretty awesome stuff.
A. N. Wenz, G. Zürn, S. Murmann, I. Brouzos, T. Lompe, & S. Jochim (2013). From Few to Many: Observing the Formation of a Fermi Sea One Atom at a
Time Science 342, 6157 pp. 457-460 (2013) arXiv: 1307.3443v2
Jeong-Hyuck Park (2013). How many is different? Answer from ideal Bose gas IC-MSQUARE conference proceedings arXiv: 1310.5580v1
I would expect, from other critical phenomena, that there would be dimensional scaling. Have the theorists done their same study in other dimensions?
Have the theorists done their same study in other dimensions?
I don’t know. I don’t think so, based on a quick scan of their introduction, but I might’ve missed something.
Critical exponents are discussed in the New Journal of Physics article. What I don’t exactly understand yet is how they achieve a discontinuity in what they claim is a finite system. Generally, you expect any discontinuity associated with a phase transition (as strictly defined in the thermodynamic limit) to be smoothed out in a finite system. The larger the number of particles, for example, the sharper the heat capacity, etc., look, but they are strictly speaking not divergent/discontinuous until “N = infty” (as the partition function is a sum of analytic functions, it can only develop a non-analyticity if you sum an infinite number of terms). But these authors claim they are getting a genuine non-analyticity in a finite-particle system. I guess I’ll have to read the paper carefully to figure out how that’s supposed to work out.