Two chapters of the book-in-progress will be devoted to the development of the modern understanding of the atom. One of these is about the Bohr model, which turned 100 this year, but Bohr’s model would not have been possible without an earlier experiment. The actual experiment was done by Ernest Marsden and Hans Geiger, but as is the way of such things, the historical credit mostly accrues to their boss and noted force of nature, Ernest Rutherford. This is the experiment that established the cartoon image of an atom as a solar system, which is utterly unworkable using classical physics, and set the stage for quantum mechanics.
The experiment itself is pretty simple: Rutherford was the world’s leading expert in alpha particles, having recently won a Nobel Prize (in Chemistry, ironically) for showing that alpha particles are helium nuclei and that alpha decay results in the transmutation of one element into another (experiments recently hailed for their simplicity in a birthday tribute to Rutherford). Rutherford had since moved from McGill in Montreal to Manchester in the UK, and was starting a program to use alphas to investigate the structure of atoms. They made a beam of alpha particles, and directed it at a thin gold foil, and then looked (literally– they detected alphas by the fluorescence they cause when they hit a phosphor screen in the beam) on the far side for alphas deflected out of the original beam path by their interaction with the gold atoms. This was expected to produce a small deviation, so they started by looking at small angles. Marsden was then an undergraduate, and when he joined the group in 1909, Rutherford suggested that they have him look to see if any alphas were scattered by a large amount. They didn’t expect any, but thought it would be a good way to get the new kid acclimated to the lab.
To everyone’s surprise, Marsden saw a whole bunch of scattered alpha particles, even at angles past 90 degrees. There were even some headed almost straight back toward the source. Rutherford’s description of his reaction is one of the all-time great quotes in the history of physics:
It was quite the most incredible event that has ever happened to me in my life. It was almost as incredible as if you fired a 15-inch shell at a piece of tissue paper and it came back and hit you.
This sort of scattering is completely impossible unless the vast majority of the mass of the atom is concentrated into a single point. The prevailing model at the time was pretty vague, but tended toward the “plum pudding” model, with the bulk of the atom being a kind of positively charged blob about an angstrom across, with electrons (known to be particles found inside atoms at that time). The positive charge was assumed to occupy the full volume, and to add up to the same total as the number of electrons, because atoms were known to be neutral. The electrons were presumed to be dotted around the interior in some manner, like raisins in a plum pudding (in the description of J.J. Thomson).
Every history you read about this talks about how the Marsden and Geiger results are completely incompatible with the prior model, but while it’s not hard to find the exact theoretical prediction for Rutherford’s model, there’s nothing comparable for the “plum pudding” atom. since I’m writing about this experiment for the book-in-progress, though, I thought it would be nice to have a side-by-side comparison of the two. So I set out to try to make one. Lacking the Godlike ability to make actual “plum pudding” atoms and shoot alpha particles at them, though, I had to settle for the next best thing: simulating the process in VPython.
The basic process is pretty straightforward, and we have sometimes assigned it as a homework/ computer lab in our E&M class. The force between the alpha particle and the nucleus is just Coulomb repulsion (both are positively charged), which is easy to calculate, and once you know the force, you can do an iterative simulation of the motion just like the pendulum simulation discussed previously. The key factor for determining the scattering angle is the “impact parameter,” illustrated in this figure from the Hyperphysics discussion:

The “impact parameter” traditionally gets the symbol b, and is basically the amount that the incoming particle is offset from a line passing straight through the center of the atom, parallel to the initial momentum of the incoming particle. So, to demonstrate Rutherford scattering, you just code up a motion simulation, input different values of b, and see what you get.
Scattering off the “plum pudding” model is harder to arrange, but the starting point is just a big spherical blob of positive charge the size of the whole atom, rather than the size of just the nucleus. But, of course, when you do that, the alpha particle has enough energy to get within the size of the atom before the Coulomb force can make it stop. And when that happens, the force drops– it’s a simple Gauss’s Law calculation to find the field of a uniform sphere of charge, which drops off linearly inside the sphere. Basically, any charge that’s farther from the center of the sphere than the position of the alpha particle no longer has any effect on the alpha. The force experienced by the alpha particle in that case is much smaller than for the Rutherford atom with all the mass concentrated in a tiny nucleus.
But it’s even worse than that, because, of course, atoms are neutral. So you need to do something to account for the electrons. I got kind of stuck here, though, because I couldn’t think of a good way to set up a real “plum pudding” arrangement that wouldn’t’ve been inordinately complicated. So, instead, I did a kind of hybrid case– I put in a spherical shell of negative charge, at a radius corresponding to the outer edge of the sphere of positive charge. This let me do a pretty straightforward comparison of the two models, and also of the effect of the electrons on the Rutherford model, which turns out to be so small it’s not worth graphing– the only difference between Rutherford model scattering angles with and without electrons is so small I don’t trust it not to be a numerical error.
So, what do the results look like? Here’s the best graph I got, a comparison of the two models (including the electron shell) for a wide range of impact parameters. The radius of the “atom” is one angstrom or 10-10m, which is probably too big by at least a factor of two, but this is such a crude model that I don’t think it matters.

The behavior here is really remarkably different, enough to make me spend a bunch of time trying to make sense of it. This is purely a result of the change in the force inside the sphere of the “atom,” so I thought for a bit that it was a coding error, but I think it’s right (the code is below if you want to play “find the embarrassing mistake”). At smaller impact parameters in the quasi-Thomson model, the alpha particle punches straight in toward the center very quickly, and the force drops very quickly. As a result, it barely gets deflected at all. At larger impact parameters, it stays more to the outside, and the force remains bigger, giving you more deflection.
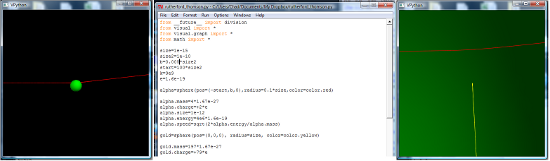
In the Rutherford case, the alpha punches through the electron shell, but never gets all that close to the nucleus– the right-hand graphic in the “featured image” up top is a zoomed-in view of the trajectory inside the shell, the red track being the alpha and the yellow the center of the gold nucleus. The force always increases as the two get closer, then, so smaller impact parameters mean larger maximum forces, and thus an increase in the scattering angle.
A sanity check on this: the two models ought to give exactly the same result at an impact parameter equal to or greater than the size of the “atom,” and indeed they do. In the case where the electron shell is present, that means a scattering angle of exactly zero (which is why there isn’t a point for it on the graph), but if I take the electrons away, I get identical results for any impact parameter bigger than the radius, which is as it should be. The scattering angles are equal at exactly the radius of the atom, and drop off as you go out farther, so there’s a maximum value for the quasi-Thomson model.
I played around a little with trying to match this to the angle behavior of the Rutherford formula, but I think I was screwing up the conversion from impact parameter to flux, and need to think more about it. I think there’s also some loss of resolution in the scattering angle calculation, which is done via an inverse trig function, and that sort of messes things up for the backwards scattering cases.
I also tried putting the electron shell inside the “atom,” at half the radius, on the thought that maybe that was more “plum pudding” like. I didn’t spend all that much time on it, though; maybe that’s a topic for another post. Several concentric shells might be the way to go for real “plum pudding” simulation, but working out how to distribute them is a little tricky, so I let it go. For now.
Another fun idea I may come back to play with: changing the size of the positive blob inside the electron shell to see how small it needs to get before you see backwards scattering.
If you want to play with this yourself, here’s my code, embedded via Gist, because Rhett recommended it; if it doesn’t work, direct your complaints to him.
A couple of little notes on this: because the scale difference between the nucleus (radius 10-15m) and the atom (radius 10-10m) is so enormous, it was really tedious to run this with a simple constant time step. I stuck in a variable time step to make it run faster: at each pass through the loop, it calculates the time step for the next iteration as the time that would be needed if you were going to cover the full distance between the two particles in 100 steps at the current speed. I did a couple of spot checks of this when I first implemented it, and it seems fairly robust. At least, the angle values it spit out were close enough to write off the differences as numerical slop. It’s possible I didn’t try the exact right case that would reveal the pathological results, though, so salt to taste.
There’s also some funny business with if statements to do the forces, and a cheap fallback on Newton’s 3rd Law to get the force on the gold nucleus. The motion of the gold nucleus makes almost no difference to the results, though. And there’s probably a better way to convert the position to an angle, but this is what I thought of first, and I didn’t bother optimizing it.
So, what’s the upshot of all this? Well, Rutherford was absolutely right to be shocked at finding alphas going backwards– using this crude method, you wouldn’t expect any particles to be scattered by an angle of even one degree for the quasi-Thomson case. A more detailed calculation with electrons distributed in a different manner might get you something bigger, but you’re not going to see anything going straight backwards, any more than you would with artillery shells hitting tissue paper.
I got kind of stuck here, though, because I couldn’t think of a good way to set up a real “plum pudding” arrangement that wouldn’t’ve been inordinately complicated.
As you’re just doing simulations, couldn’t you just randomly place point charges within the sphere of the atom, and average over multiple replicates with different arrangements of point charges? If the exact electron distribution doesn’t make much of a difference, the spread should be pretty tight, with perhaps the occasional outlier when the path takes you directly over an electron. If the exact electron distribution *does* make a big difference, then approximating it as a uniform spherical shell will be misleading at best.
Coming out of high school and college, I had a penchant for analytical approaches to problems. It was rather eye-opening when I realized how much easier some problems become when you say “to heck with it”, and simply iterate the snot out of them with different random starting conditions. Ulam was one clever cookie.
See, I would regard randomly placing 79 electrons within that volume as inordinately complicated… I agree that it would be a good way to go about the problem, but it just seems like too much work.
I’ve also never been clear on whether there was believed to be structure within the plum pudding model. Textbook pictures are always kind of random and blobby, but that doesn’t really seem consistent with the general approach of the time, or physics itself. Concentric shells of regularly spaced electrons or something would seem more likely. But then, I’m not sure it was ever developed all that fully before Rutherford/ Marsden/ Geiger blew it away.
An interesting next step would be to plot the distribution of scattering angles for the two cases, assuming the impact parameter is uniformly distributed. Maybe on a polar plot?
Also, I think the function atan2(x, y-b) could help you avoid that if/else statement at the end.
Of course, google is your friend
FWIW, the best story Eli knows about the Rutherford scattering experiment is the Geiger got pissed off siting in a dark room looking for flashes on a scintillator screen when he could be out partying in Montreal so he invented the Geiger counter.
OTOH, Rutherford’s demonstration that alpha particles were He nuclei was in many ways more impressive and just as important
You should really mention that the deflection angle also depend on the energy of the incoming alpha. That is, the graph that you show comparing Thompson and Rutherford is for a particular energy. It looks like your code is in MKS, so the initial incoming speed of the alpha is roughly .05c. Is that realistic for the kind of experiments Rutherford was doing?